Collaborative Filtering에는 두가지 방법이 있다

1. 이웃 기반 방법 (Neighborhood-based Method)
- 영화 선호도의 유사도에 기반하여 이웃을 탐색
- 찾아낸 이웃들이 시청한 영화를 추천
2. 잠재 요소 방법 (Latent Factor Method)
- Low-dimensional (latent) space에 유저와 영화의 성질을 표현
- 유저와 근접도(proximity)에 기반해서 영화를 추천
- Goal : 유저와 영화를 latent space에 잘 임베딩 하는 것
Matrix Completion(MC)
MC는 CF에서 널리 쓰이는 태스크이다.
먼저 유저의 아이템에 대한 explicit feedback을 고려한다. 미완성(incomplete)인 user-item rating 행렬을 user/item 행렬들로 분해한다.

Notation
- \( R \in \mathbb{R}^{m \times n}\) : Rating matrix
- \( \Omega (R) = \{ (i,j)|R_{ij} \neq 0 \} \) : non-zero (or observed) entries 의 집합
- \( U = [ u_1 ; \cdots ; u_m] \in \mathbb{R}^{m \times d} \) : User matrix
- \( u_i \in \mathbb{R}^d \) : \( i\)번째 유저 벡터
- \( V = [v_1; \cdots ; v_n] \in \mathbb{R}^{n \times d}\) : Item matrix
- \( v_j \in \mathbb{R}^{d}\) : \( j\)번째 아이템 벡터
- \( \hat{R}_{ij} = u_i^{ \top} v_j\) : Rating prediction of user i on item j (inner product)
> Basic Objective for MC

- Reconsturction Error : observed matrix entries 만 고려
- Regularization : params를 줄여서 모델이 오버피팅 되는 것을 방지
손실함수만 이용해서 값이 작아지는 방향으로만 모델을 최적화 하게 되면, 특정 가중치가 너무 큰 값을 가지게 되어 모델의 일반화 성능이 떨어지게 된다. 즉, 오버피팅 되게 된다. Regularization은 이렇게 특정 가중치가 너무 과도하게 커지지 않도록 하는 역할을 한다. [1]

두 엔티티 사이의 유사도가 높으면 Reconstruction에서 두 엔티티 사이의 거리를 좁힌다.
PMF (Probabilistic Matrix Factorization)
Salakhutdinov and Mnih, Probabilistic Matrix Factorization, NeurIPS 2007
- Likelihood of Observed ratings(주어진 factor 행렬) : 가우시안(정규) 분포에 기반

가능도(likelihood) [2]
어떤 값이 관측 되었을 때, 이것이 어떤 확률 분포에서 왔을지에 대한 확률.
즉, 고정된 관측값이 주어졌을 때 해당 확률분포에서 나왔을 확률을 말한다.
likelihood = L( 확률분포 D | 관측값 X)
- User/Item latent vector : zero-mean spherical Gaussian priors 라고 가정

- Log posterior distribution over U and V
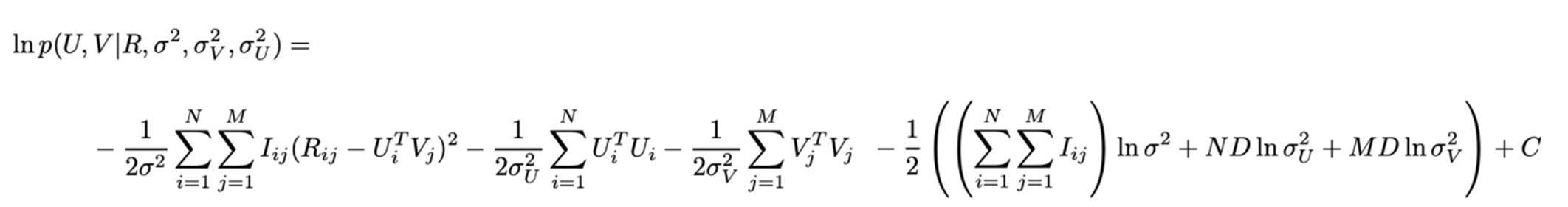
Posterior : 관측값(R, σ)이 주어졌을 때 구하고자 하는 대상(U,V)이 나올 확률 [3]

PMF의 목표는 하이퍼파라미터(\(\sigma \), \( \sigma_U\), \(\sigma_V\))를 고정시킨 채 log-posterior 를 최대화 하는 것이다.
이는 (1) sum-of-squared-errors-objective function과 (2) quadratic regularization 을 최소화 하는 것과 동일하다.

> 손실함수를 최소화 해주는 U와 V를 찾는 방법 : MC Solvers
1. Stochastic Gradient Descent (SGD) \(\Rightarrow\) Data Parallelism
랜덤하게 observed matrix를 선택해서 해당되는 모델 파라미터들을 계산된 gradients에 기반하여 업데이트 한다.
Iterative update for each observed rating
2. Alternating Least Squares (ALS) \(\Rightarrow\) Model Parallelism
각 factor matrix를 alternately 하게 업데이트 해서 objective function을 최소화 한다. 이때, 다른 factor matrix는 고정시킴.
Iterative update for each model vector
3. Coordinate Descent (CD) \(\Rightarrow\) Model Parallelism
한 번에 한 파라미터를 업데이트를 한다. 이때 다른 변수들은 고정시킴.
Iterative update for each model parameter

[Data parallelism]
1. SGD (Stochastic Gradient Descent )
Korean et al., Matrix Factorization Techniques for Recommender Systems, Computer 2009
알고리즘

observed 된 Rating matrix에서 학습시킬 포인트 (i, j)를 골라 해당되는 유저 메트릭스와 아이템 메트릭스를 업데이트
2. DSGD (Distributed Stochastic Gradient Descent)
Gemulla et al., Large-Scale Matrix Factorization with Distributed Stochastic Gradient Descent, KDD 2011
DSGE는 처음으로 interchangeability의 개념에 기반한 parallel SGD 방식이다.
만약 SGD를 업데이트 하는 순서가 최종 결과에 영향을 미치지 않는다면, matrix entries (i, j) 같은 data object의 쌍을 interchangeable pair라고 한다.
어떠한 포인트 \(p_x \in X \)와 \( p_y \in Y \)가 interchangeable 하다면, 두 블록 X와 Y가 interchangeable 하다.
전체 메트릭스를 \( d \times d\) 로 나눠, d개의 블록들에 parallel update를 한다.

3. FPSGD(Fast and Parallel Stochastic Gradient Descent)
Zhuang et al., A Fast Parallel SGD for Matrix Factorization in Shared Memory Systems, RecSys 2013
FPSGD는 non-locking 스케쥴링 알고리즘으로 최소 (p+1)-by-(p+1) grid를 사용한다.
(p+1)-by-(p+1) 를 사용하기 때문에 추가적인 free block이 항상 존재하게 된다.
이 free block은 쓰레드에 의해 업데이트 되지 않지만, 업데이트 되는 모든 블록들과 interchangeable 하다.
non-locking 스케쥴링은 업데이트 되는 횟수가 가장 적은 새로운 블록을 할당하게 된다.
또한 이 방법은 블록에서 sequential 하게 entries를 선택해 memory continuity를 달성한다.
Space locality(공간 연속성) 활용 가능.

4. NOMAD
Yun et al., NOMAD: Non-locking, stOchastic Multi-machine algorithm for Asynchronous and Decentralized matrix completion, VLDB 2014
NOMAD는 ownership of update의 개념을 도입했다.
Row 인덱스들을 파티션으로 나누고, row (\(u_i\)) 를 위한 ownership of update는 각 파티션에 해당되는 workers에게 할당된다. 그리고 이 파티션은 실행 동안 변하지 않는다.
Column (\(v_j\)) 을 위한 ownership of update는 worker들 사이에서 교환된다.
미리 지정한 횟수의 업데이트가 진행된 후에, worker들은 비동기화 message passing을 통해 ownership of update for columns를 서로에게 넘겨준다.

5. MLGF-MF
Oh et al., Fast and Robust Parallel SGD Matrix Factorization, KDD 2015
MLGF-MF는 rating matrix를 Multi-Level Grid File (MLGF)로 관리한다.
이 방법은 각 데이터 블록의 observed entries 개수를 balancing 해서 skewed matrix를 robust update 하도록 한다.
즉, Balance Data Block 을 통해서 파라미터의 수(# of entries)를 balancing한다. 이 Balance Data Block은 파라미터 수에 상한선을 정해서 partitioning을 한다.
이 방법은 MLGF에서 partial match queries를 통해 효과적으로 non-interchangeable 블록들을 retrieve 할 수 있다.


[Model parallelism]
1. ALS (Alternating Least Squares)
Zhou et al., Large-scale parallel collaborative filtering for the Netflix prize, AAIM 2008
MC를 위한 objective가 non-convex 해도, U와 V를 고정시키면 이 objective를 이차방정식 문제(quadratic problem)으로 만들 수 있다.

V를 이용해 U를 업데이트. 모델의 벡터를 업데이트 한다.

하지만, ALS의 업데이트 규칙은 computationally-expensive한 matrix-inverse operation을 포함한다.
2. CCD (Cyclic Coordinate Descent)
Yu et al., Scalable Coordinate Descent Approaches to Parallel Matrix Factorization for Recommender Systems, ICDM 2012
CCD는 MC를 위한 효율적인 CD 방식이다.

다른 모든 파라미터들을 고정시키고 optimal 한 값인 \(u_{it}\)는 다음과 같이 계산한다 :


residual 메트릭스와 모델 파라미터는 다음과 같이 업데이트 됨 :

Tensor Completion(TC)
Tensor : 데이터를 표현하기 위한 고차원 array
- MC : MF, SVD(Singular Value Decomposition)
- TC : Canonical Polyadic (CP) decomposition, Tucker Decomposition
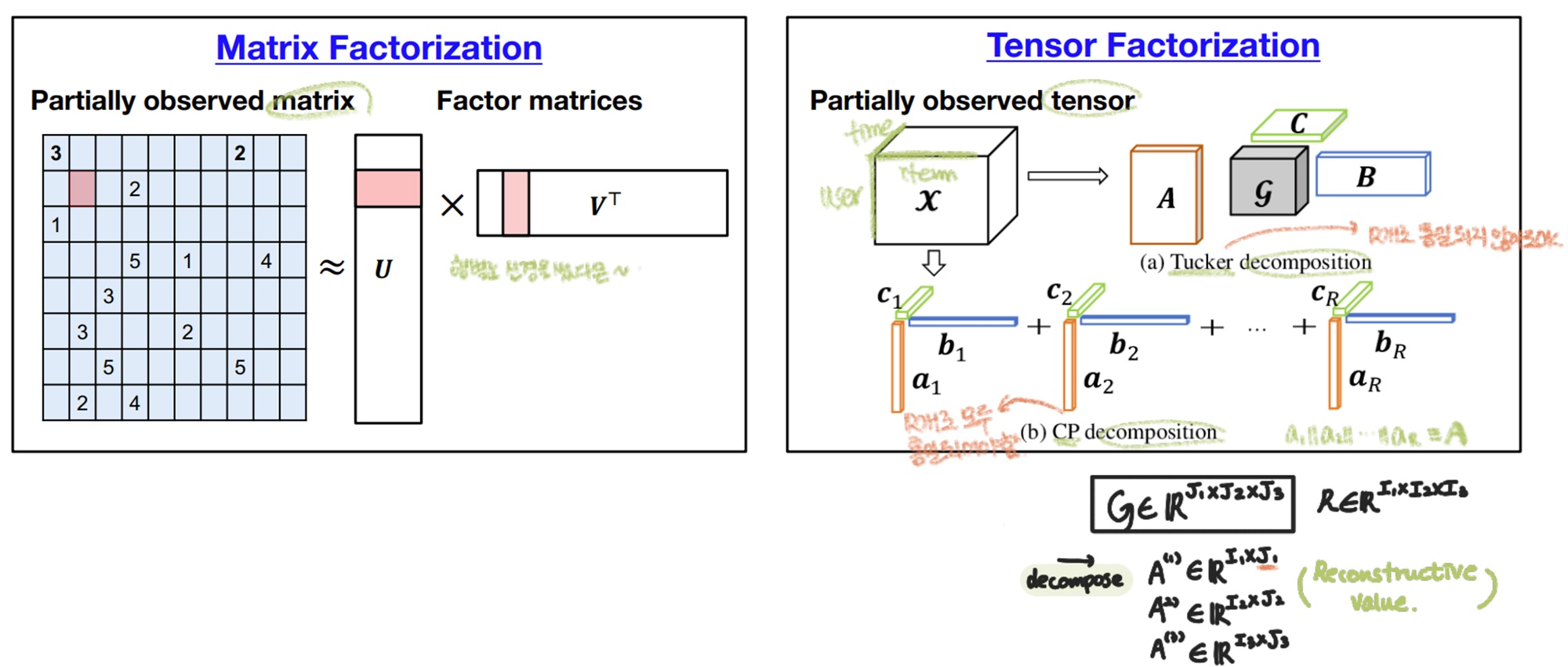
TC는 MC와 비슷하다.
Factor Matrices \(\{A^{(n)}\}\) 는 MC처럼 SGD, ALS, CD solver들로 최적화 할 수 있다.

> Canonical Polyadic (CP) decomposition
CP decomposition은 tensor를 factor matrices로 분해한다.

> Tucker decomposition
Tucker decomposition은 tensor를 core tensor와 factor matrices로 분해한다.
CP decomposition은 Tucker decomposition에서 \( \mathcal{G}= \mathcal{I}\)인 특수한 경우이다.

참고
[1] https://light-tree.tistory.com/125
딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명
제가 공부하고 정리한 것을 나중에 다시 보기 위해 적는 글입니다. 제가 잘못 설명한 내용이 있다면 알려주시길 부탁드립니다. 사용된 이미지들의 출처는 본문에 링크로 나와 있거나 글의 가장
light-tree.tistory.com
[2] https://jjangjjong.tistory.com/41
확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)
* 우선 본 글은 유투브 채널StatQuest with Josh Starmer 님의 자료를 한글로 정리한 것 입니다. 만약 영어듣기가 되신다면 아래 링크에서 직접 보시는 것을 추천드립니다. 이렇게 깔끔하게 설명한 자료
jjangjjong.tistory.com
[3] https://aimaster.tistory.com/79
Posterior, Likelihood, Prior
베이즈 정리를 구성하는 Posterior, Likelihood, Prior가 헷갈리는 이유는 각각을 구분하는 기준을 아직 모르기 때문이다. 우선 셋을 구분하기 위해선 문제 해결을 위해 구하고자 하는 대상, 주어진 대
aimaster.tistory.com

